19 SP-D trimers (AFM images from several published articles) were counted many different ways to determine peak number. These methods have been described many times in previous posts.  135 plots (129 of which were images that had NOT been filtered, and one image (trimer – 1) which had an additional plot from a gaussian blur (5px)).  The three columns below represent (left) my count of bright peaks directly from the image, (center), my division of the grayscale plot (done in imageJ),  and (right) the 5 signal processing apps applied with consistent functions over the images. The data show “more” peaks found in the signal processing group which also showed a larger standard deviation, also a few more peaks found observing the csv plots, and the fewest (though not significantly fewer than the hand counted peaks from plots) as they are seen in the image. The mode and median from the image and the ImageJ plots are the same. There are differences in each of the signal processing apps, enough so that the peak finding in the whole dataset does not make a normal distribution.

When each of the 5 (plus my counts)=6 peak finding apps were analyzed separately  the difference was seen below.  On the left, my peak determination from grayscale plots obtained from ImageJ, and right, each individual peak finding apps  (the same apps used previously in this blog) applied to each of the 19 trimers, so the total n of plots is still 135, but the n of 6 is the number of different apps used to detect peaks.  The distribution of means and SD from the 6 individual signal processing apps does form a normal distribution.  The difference between the mean of the peaks i count from plots, and the peaks found using signal processing is significant with a 1-tailed t test, (p=.032) but not with a 2 tailed t test (p=0.065).

The next step is to apply image filters to each trimer, and to each of those, apply the signal processing apps to find concensus.  Seems to me that the data will fall inbetween ….  not 7 not 9  but “8” which would be predicted from the similar assessment of dodecamers (plotted as hexamers)… of which I have plotted hundreds and hundreds  (LOL).

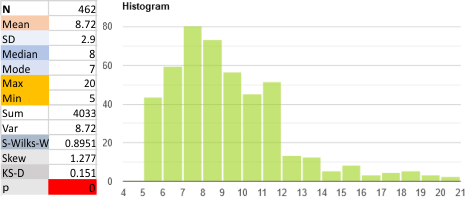
I couldnt resist plotting every peak count for these 19 trimers so far…. also, not a normal distribution. The outliers (15 peaks to 21 peaks) all arise from signal processing the plots (yes i could manipulate the functions and make them all 8 peaks, but it seemed to me to be a more honest approach to find a setting and stick with it).  The highest peak counts came from Scipy, and iPeakM80 (Octave). I wonder about the efficacy of changing those parameters to fit my “idea”.