Fun with Copilot — SP-D dodecamer — no where near reality:
I asked Copilot to generate an image of a Surfactant protein D dodecamer as seen by atomic force microscopy thinking that the image that have been published, mainly by Arroyo et al, would have sparked some kind of realistic image, first pop, here is what came up. Not atomic force microscopy but some kind of conglomeration of a molecular model.
a surprise to say the least, not partiularly a good surprise. Looks like dredlocks to me.
I adked again mentioning that I didnt want a ribbon molecule of just the carbohydrate recognition domain, to please try again. I mentioned that it had three trimeric arms, and was shaped like an X.
Try 2 with Copilot was not much closer to the images actually shown with AFM. 
Try 3. This time i mentioned that most atomic force micrographs have an orange, deep red, and bright yellow coloring, and the the arms of the SP-D dodecamer were long, and here is what was generated.
 Try 4. I mentioned that the arms were not wide on the dodecamer, and that the N termini were joined together in a bright peak in the center of the dodecamer, and here we have —
Try 4. I mentioned that the arms were not wide on the dodecamer, and that the N termini were joined together in a bright peak in the center of the dodecamer, and here we have —
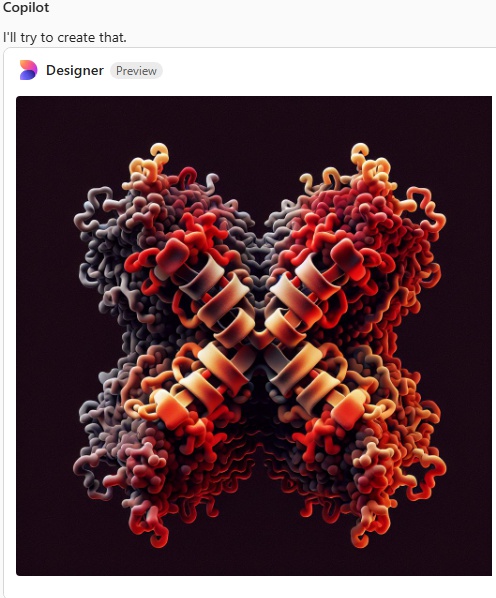 I am a little surprised that since there are so many image of the SP-D X shape, and so many references to the alpha helix in the neck (and adjacent collagen like domain) that this image still looks like a form of spagetti. I am pretty sure i mentioned that the trimeric arms were identical which apparently Copilot did understand.
I am a little surprised that since there are so many image of the SP-D X shape, and so many references to the alpha helix in the neck (and adjacent collagen like domain) that this image still looks like a form of spagetti. I am pretty sure i mentioned that the trimeric arms were identical which apparently Copilot did understand.
Try 5. Arms are indeed a little thinner but there is nothing at all that looks like an alpha helix, and totally missing is any appearance of the three carbohydrate recognition domains that flop around as the three C term elements of the trimer…. that also is open information in terms of molecular models and diagrams.
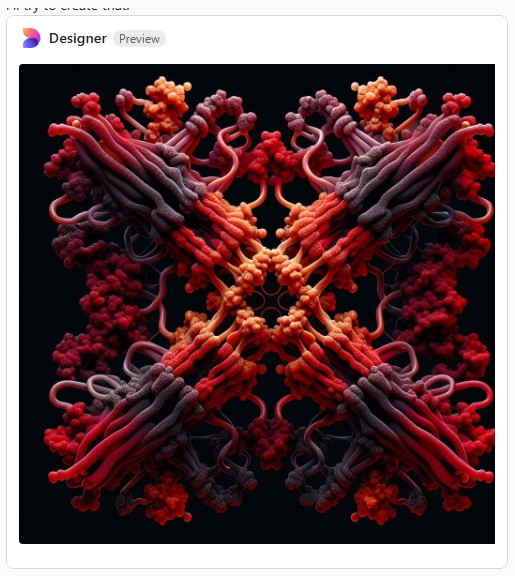 Try 6. This made me laugh, and it also must have frustrated Copliot, cause that was the end of the exploration, I guess I had used up to much valuable time. LOL, this looks like something from a restaurant that sells gourmais deserts.
Try 6. This made me laugh, and it also must have frustrated Copliot, cause that was the end of the exploration, I guess I had used up to much valuable time. LOL, this looks like something from a restaurant that sells gourmais deserts.
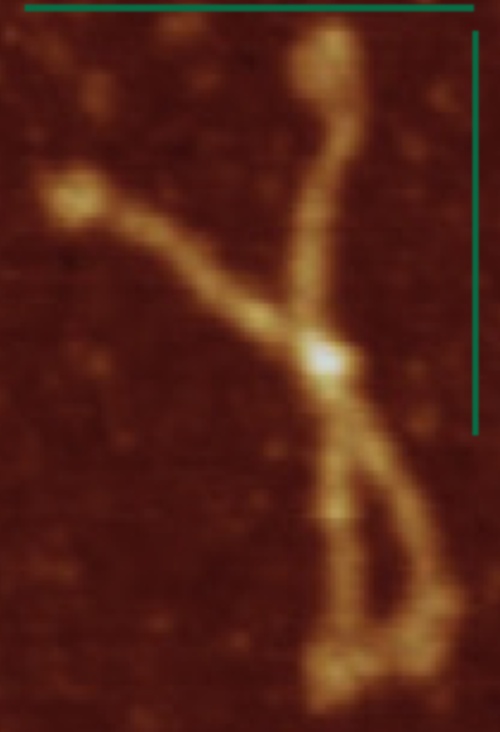
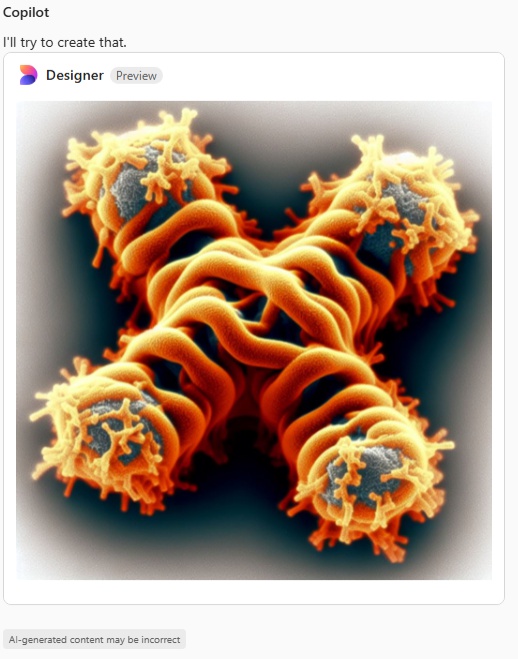 Here just for the record is one of the very nice atomic force images of SP-D produced by Arroyo et al, which I have worked on to determine how many peaks per trimeric arm are present.
Here just for the record is one of the very nice atomic force images of SP-D produced by Arroyo et al, which I have worked on to determine how many peaks per trimeric arm are present.