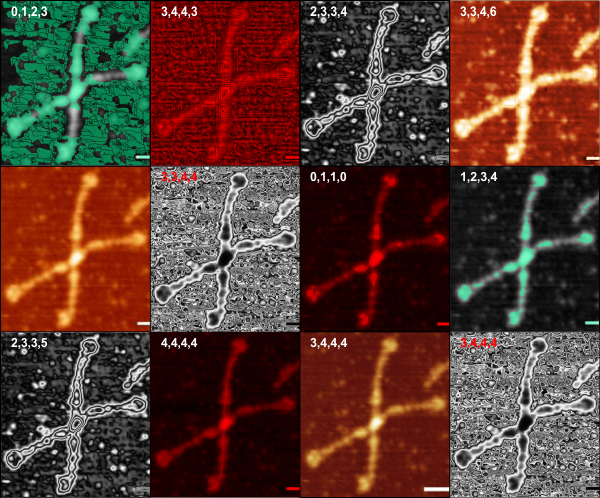
Does it matter which algorithm you use, or should you use your common sense? Grappling with how to go about determining the number of peaks in collagen-like segment of SP-D just seems to be best done by the person looking at the micrograph.  I am trying out a new program, Gwyddion, and it makes really nice pictures, no question, its not that easy to use in my humble opinion, but it seems to have some advantages over using CorelDRAW alonside ImageJ (FIJI) but some annoying disadvantages as well.

(Aside from being more for the person who wants to customize image processing, there is nothing that the “visual” based learning experience can benefit from here, except perhaps from approaching the program with trial and error (pretty much what i did, trying to get some data from the process along the way).

I am struck by the divide in cortical processes between the programmer mind and the microscopist’s mind, and a little incensed at the arrogance when interfaces are (as they claim are intuitive thereby attributing some degree of ineptitude on one who views it otherwise. This, like many other professional venues, select for a specific trait.)

For me, it has not proven useful to use any of the image processing programs (ImageJ, J2, FIJI or Gwyddion, photoshop, CorelDRAW) to confirm or refudiate the presence of peaks along the collagen like domain of SP-D. Hundreds of plots later, i still get a mix of 3 to 4 peaks.  In the above, mean number of peaks in that region was 3.  There are a few pix i would remove since i actually think there are four peaks.  Bias is an easy thing to introduce, but no bias skews the results when applied randomly as in these images.  Original image is from Arroyo et al’s paper and also the same image is in supplemental figure 4.

Count, N: 47
Sum, Σx: 144
Mean, μ: 3.06+1.29
Variance, σ2: 1.67

Below…   the two images which really dont help resolve the peaks in the collagen-like domain have been excluded. One wonders how to explain bias if I pick the best representations. It is something like what one experiences when doing stereology on a circle, where one rarely finds the optimal diameter, and in this case the optimal peak number, so all values need to be evaluated with this in mind.

Count, N: 41
Sum, Σx: 143
Mean, μ: 3.48+0.85
Variance, σ2: 0.73

How often does optimal “happen” in the preparation of SP-D. Establishing the right number of samples – finding the right (maybe several) approach to measuring.