There is often a slight decrease in the N term peak, likely where the N term domains join the trimers at the center of the dodecamer. This is an infrequent event and its detection is also related to how one draws the plot line through the center of the image of the molecule.  When the N term peak width is listed there are occasions when it interferes (reduces) the total N term peak width. The tiny change in grayscale (height and valley) of the N term peak is pretty small. I have put a ? in the title of this peak to denote its inconsistent appearance.

It is nevertheless listed here in a graphic and below, it appears in two of the eight trimers in these data.

Same MO,  but since this peak appears 100% of the time (so far) there is no second column where the mean (and other parameters) is calculated excluding the missing (undetected) peak values.  Difference in CRD peak width is certainly not very different from the first 6 dodecamer summary than the first 8 dodecamer summary. Some benefit is gained by using the means of each, rather than the individual trimer values.

Same MO.

Same MO as previously .  In my own observations I have seen this broad low peak as a consistent feature, perhaps more consistent than peak 5.

These data were derived using the not-detected peak values (listed as 0s) included in the whole sum, and also with the not-detected peak values.  Those data without the missing values are indicated with a “yellow” color in the cell.

I am actually glad that the data dont change much regardless of whether it includes the 6 dodecamers, or the 8 dodecamers, or the missing values, clearly the data are pretty stable.

Images below (top two image are the summary of all the trimers counted (six, and eight trimers). Peak 5, (color has been pink in every post for the last two years) is a thin and low peak which is present in  Values include each trimer plot  as well as the dodecamers as single entities (n=6 and n=8).  72.5 (six dodecamers) and 74.4 % (eight dodecamers) of the time, peak 5 is detectable.  A nice round number for the width of peak 5 is 5nm.

Each dodecamer is treated separately and data are listed below the summary tables.

As Before.   Peak 5 is adjcent to the glycosylation peak, and often seems to be a little less high, and a little less broad.

as before, mean is in nm as determined from the micron bar in each image. So the glycosylation peak seems to be just about 18 nm in width, as shown by measurements on the first 8 dodecamers (AFM images plotted in IMAGEJ, with images subjected to many different filters, and plots subjected to many different peak finding programs.

Same modus operandi. Peak width might be just between 4 and 5nm +/ 1nm wide when calculations are made without the undetectable peaks. Measurements of just the peaks that appear will be done henceforth.

In this assessment of N term peak width, two new sets of measurements have been added. The caveat here is that both the image I have labeled 4A (supplement figure 4, image A from Arroyo et al) is also the image that I have named 127 (from the body of the paper, thus a different resolution, different bar marker, different ppi, and different contrast and HSL, image processing filters, (but NOT different peak finding apps).  These are sort of used to compare differences between random image factors (you can make your own comparison just by looking at the statistics for 4A and 127 in the figures below). A two-tailed t-test determines: The t-value is 6.57159. The p-value is < .00001. The result is significant at p < .05 between the two sets of data. They are not out of line with means for N term width for other N termini peaks.

Means for the N termini peak of n=six dodecamers, and n=8 dodecamers is the top figure. And individual dodecamers are listed in the two figures below (by the names I have given them, and also color coded).

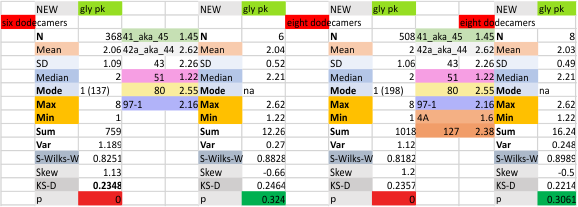
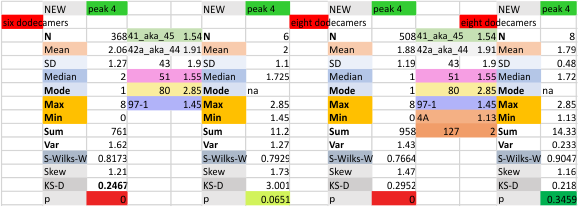
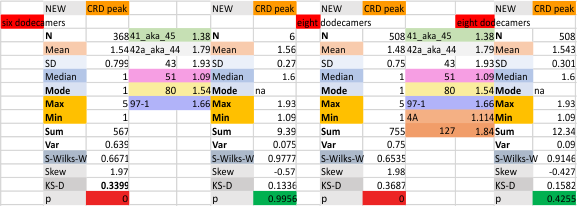
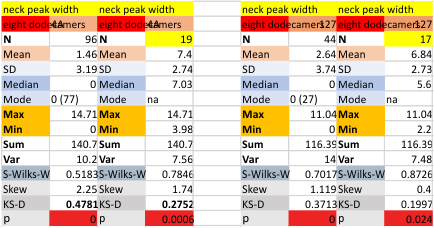
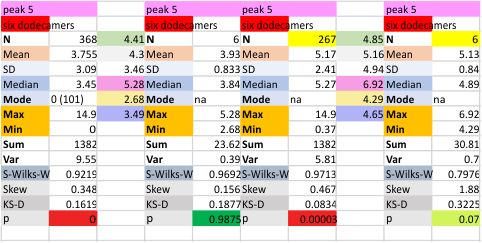
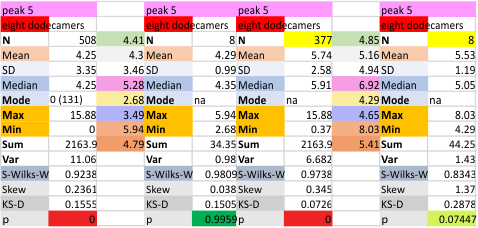
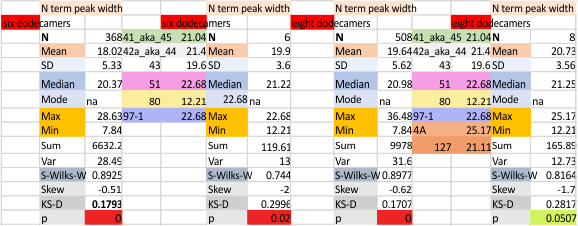
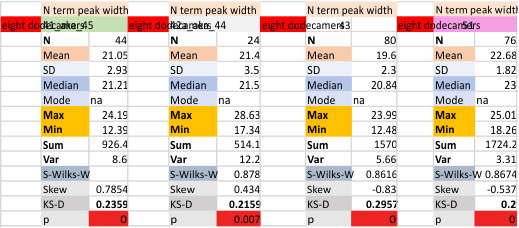
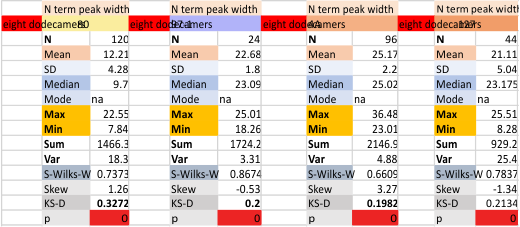
These data show the number of smaller peaks within the tracings of SP-D trimers (using AFM images from various published papers). At this point they are all rhSP-D images. The trimers are plotted beginning at the most complete side of the N term peak. This means that the whole N term is plotted (and it includes the N from the adjacent trimer(s) that build a dodecamer. All these plots are from dodecamers. This link is to a summary of the number of sub-peaks.
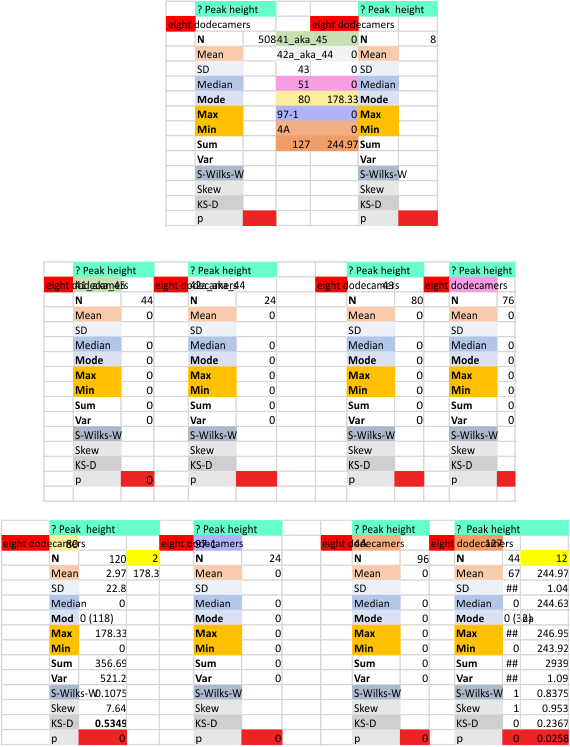
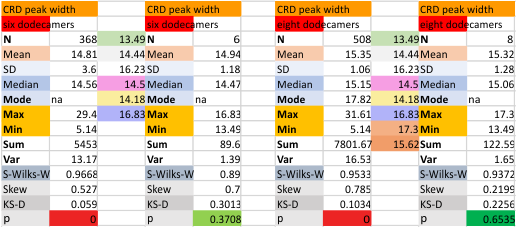
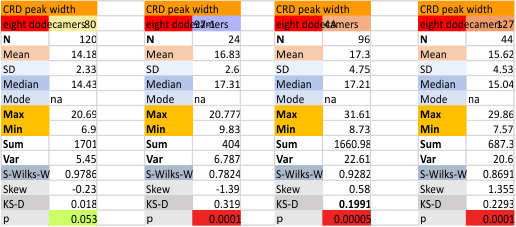
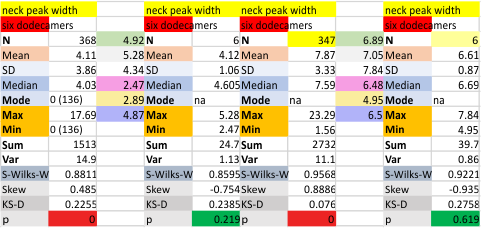
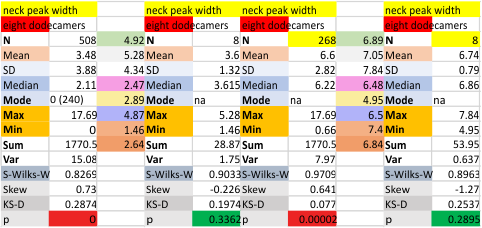
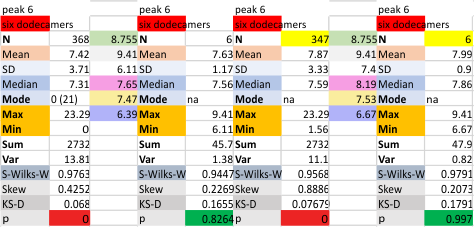
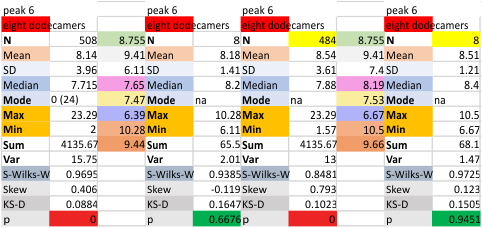
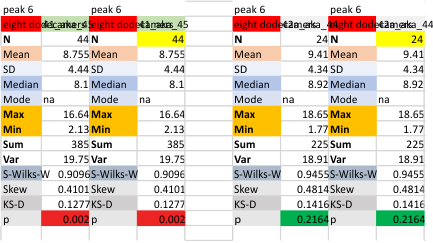
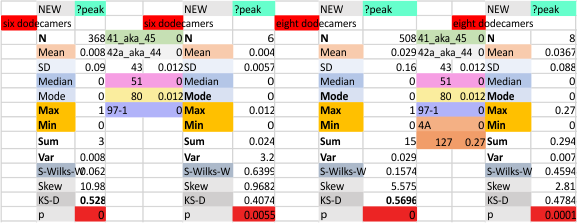
It has been my observation that the multimers of SP-D with higher than four trimer arms often show a decreased brightness within the center, and many images confirm this. In this series of plots there are just a few images where in a plot of a hexamer, there is a small peak in the center of the N term peak. I have labeled it the ? peak, and it is shown below in light bluegreen.  It doesn’t occur often but enough to mention it. All the data are organized similarly. On the far left is the sum total of peaks from six hexamers (n of trimers =368 which includes gray  scale plots from many signal and image processed images, so on the very left, no division into dodecamers is made, but the column just to the right of that has six dodecamers where the mean occurrence of peaks is found where the N=6.  On the right hand side of the data, far right, the same has been applied to 8 dodecamers, and just to the left of that set of numbers is data for each individual trimer, and n=508 plots.
While signal processing apps have determined that there are likely 15 peaks per hexamer, this number does NOT include the ? peak above.

The 8 peaks per trimer (N peak is counted once with each trimer, but also counted only once with each hexamer) are as follows:

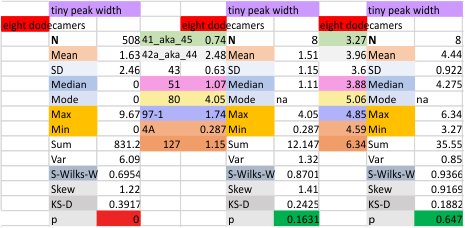
N term peak, tiny unidentified peak, glycosylation peak, peak 4, peak 5, peak 6, coiled neck peak 7, CRD peak 8, and are labeled like this below. The means are the number of sub-peaks per peak.  The three confirmed peaks (in the literature are N, gly and CRD, the neck peak 7 is inconsistent because the CRD domains obstruct it often. Peaks that are NEW, and as yet unconfirmed are tiny peak (2), peak 4, 5, and 6).

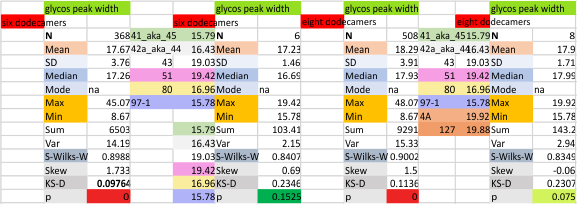
The N term peak has been organized with the mean of the sub-peaks per N term peak plotted from the same trimers as above. And so on, for each of the peaks — as listed above.

The glycosylation peak is apt to be not just one peak but two (and my thought is because each of the trimers can by glycosylated individually, and the coil of the trimer ofsets each of those sub-peaks.  Those peaks composed of more than one sub-peak are the glycosylation peak (peak 2) and an as yet undescribed peak 4 which also has two sub-peaks.  The CRD domain is subject to a different type of flopping around, and does not show two peaks consistently. This is likely affected by the fact that a plot line goes through the CRD often not picking up the apparently random order that the CRD domains of the trimer fall during processing.