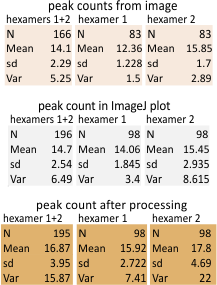
Finding peak height and width from image plots (ImageJ) and signal processed plots (Octave and Excel templates)  can be done, but by and large, trying to figure out any details for where the markers for the widths of the peaks  in the signal processed plots is no better than doing it by hand, EXCEPT for one excel program which is free to anyone developed by Thomas O’haver, and is called PeakValleyDetection.  This program allows a new series to be plotted which shows the valley marks on the plot.  For me, this is the best program so far for determining where the valleys are “without my personal input”.  Looking for valleys and peaks in all other measurements seems to be a mattern of “selection” by the user.

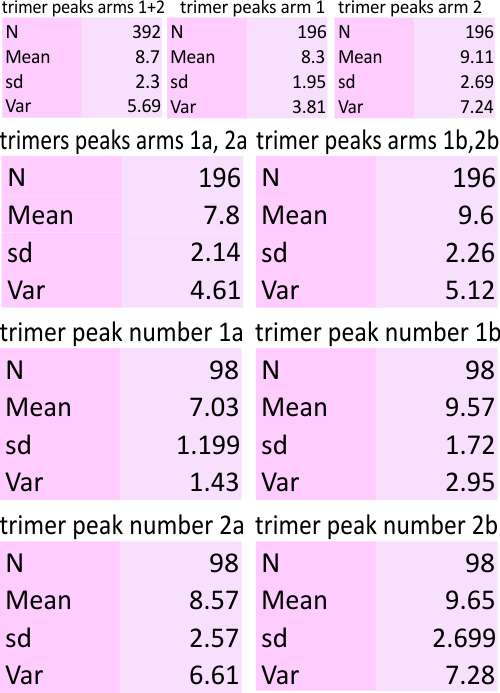
Here is an example. 1) original image and plot using ImageJ, 2) plot from image J smooth using PeakValleyDetectionTemplate-xlsx, 3) comparison plots from my choice of valleys and peaks within the ImageJ plot and the valley choices made automatically by a smooth factor of 11, in the PeakValleyDetectionTemplate-xlsx. They are close.  I made some different choices, and the algorithm made some as well. One issue with the xlsx template is that it tends to leave off (or not count) the last peak. I dont think this is a good thing, but I bet that the problem is that it uses a “backlooking” perspective and does not account for the fact that in biology there is so much repetition (mirror, duplication, inversion, tandem, bilateral, etc etc ad nauseum) that iterations of a pattern are not taken into account like they should be.  This is one of the reasons that the plots were analyzed as trimers separately.

OK, a new issue just came to mind – and that is a) the segmented line used for plots always went from left to right, and therefore in the algorithms, there may be some bias, whereas with the human eye, probably not.  So that begs the question, if i plot all trimers outward from the complete N termini peak, will this change the results in those plots which plotted in the mirror of each other.

This is the beginning of width and height counts for the summation of numerous measures of many image and signal processed plots for a single dodecamer. (see previous posts) and image of the actual dodecamer at the end of this post – a guide to labels and names used in the summaries).

Starting with the width of the N terminal peak which is a junction of four N terminal domains from each of four trimers, thus 12 parts. Results in nm (calculated from the bar marker in the original image).

No variation here in the width of the N term peak regardless of how one measures it. It appears that going from one side to the other within the context of each arm shows an even and regular arrangement of the three trimeric N’s.  When measured individually, the same results appears. Some of my original counts did NOT include a tiny peak on either side of the N term juncture and this accounts for the change from @20 nm width to the current value of @15 nm.  The appearance of that tiny peak resulted from the use of signal and image processing tools.

Just to reiterate: these are all values from analysis of a SINGLE SP-D image (noted many times before in this blog). Various methods of enhancing the image for detecting peaks (whether by filters and masks in photoshop, corelDRAW, or corelDRAW photopaint, or Gimp or gwyddion, and several more raster adjusting programs, as well as a few signal processing programs (PeakValleyDetection xlsx, PeakDetection xlsx, Octave (ipeak.m, findpeaks.m, allpeaks.m), there is concensus. IT IS CONCENSUS BY CHOICE. It has to be recognized that the CHOICE, whether of filters and masks in image processing, or functions in signal processing, is mine (YOURS). Peak counts can be manipulated to go from 1 to 40 in both image and signal processing. It requires sensible input from the user.  That said – 15 peaks per hexamer looks pretty solid.

Here are the N, mean, sd, var for trimer peak counts – which numbers include the processing that has been done so far, so this will change with other variations on the signal processing data. Please note that the complete N terminus peak is included in the counts of every trimer (this means that from the distal edge of the center bright peak to the CRD is what is measured, so counts include the whole N term of the dodecamer as a ONE peak) in each trimer.